简单做一下今年的阅读计划。

• 书籍:

• 电影：

• 舞剧：

• 演唱会

未完待续

yield

seaborn

数据可视化[https://www.cnblogs.com/kylinlin/p/5236601.html]

时间过得确实好快，一转眼就毕业了，然而和四年前一样我居然还留在哈尔滨= =。随着大学毕业，我也就正式成为了一名社会人(不赚工资的社会人)沉迷毕业已经有段时间了，然而真正值得纪念的难道就不能再见了么。。。其实还是很容易的吧，总是不想和自己学生的身份告别，所以今天我丫正式成了一名社会人。

本来，我明天就到NUS了吧。

大学一毕业，好像很多遗憾就没了一样。多出来的只有毕业的遗憾，虽然有点绕口。

Game Over.It’s time to be strong.

0.

最后还是咸鱼的没有申请选择了国内读研

1.

结束了在iflytek的实习，也算在工业界里待了大半年。这半年周末过的很浪啊= =

2.

毕设可能要做不完了

3.

办了个私教，anyway希望毕业前能瘦到来的时候的体重

4.

第一次去美帝玩了趟，见到了大都市。却没有想留在那里的想法

5.

参加百度的阅读理解，可能是弥补一下水的不行的毕设吧

6.

自实习后，时间利用率稍有提高，但也只仅限于小学生水平，想法变少了，大概就是社会化了吧

7.

确实没有大智慧，喜欢耍耍小聪明，希望可以变得稍微勤奋点。另外似乎找到了学习上的一个大毛病。。

8.

艰难地水完了一篇总结，最后大学里的三个月，恰逢现在是三月份，就叫疯狂三月吧

to do list

毕设

百度阅读理解

深入理解计算机系统

ml&dl

To do list

CS224

to do :

• Lecture one and two suggested readings and python tutorial

done :

• Lecture one vedio
• Lecture twon vedio

深入理解计算机系统

to do :

• chapter one

done :

• ~~[49/775]~

Machine Learning

to do :

• SVM

done :

• [128/382]

计算机网络

to do :

• TCP

Done list

• Sorry , Nothing

                                                            Update until 9.19 a.m.

Put more on what you good at and put more on what you like.

嘻嘻哈哈

又到了不定期更新blog的时间了，趁着最近比较轻松(xian)，写点没人看的羞耻blog吧 = =

保研？出国？工作？

      其实离做最终决定的deadline还有两天，是不是就说明了我还有还有可以继续考虑。怕是下定了主意了。前几天回家的车上看了一部电影《三个老枪手》，反思自己的人生是不是也是一成不变的，人生的际遇谁又能说的准。说实话，我倾向毕业直接工作的概论都大于出国了。如果不是出去读PHD，美国的诱惑也没有那么大。读PHD的内因又不是自己真的对某个领域特别感兴趣，反而是一些外因起到了作用。别人说的话自己听听可以，决定还是要自己来下。那么先放下自己的幻想吧，姑且先用幻想这个词。人生除了仰望星空，还是要脚踏实地。明明就不是适合读博的人，还去赌博就不会是一个好选择了。

旅游！

      其实对12月份的旅行还是很期待的，大学期间没特意出去旅行过，只是随着到处打比赛去过几个地方。准备玩个20天，从某种程度上也算践行了之前出国的打算。下周约了个面签，希望一次就能签过吧，周日晚上再来个三方会议，敲定一下旅行城市和行程。

实习~

范数

    有时我们需要衡量一个向量的大小，在机器学习中，我们常使用被称为范数(norm)的函数衡量向量大小，形式上$L^p$范数定义如下：
$$||x||_{p}=\Bigl(\sum_{i}|x_{i}|^p\Bigr)^{\frac{1}{p}}$$
其中$p\in\Bbb{R},p\ge1$。

    范数(包括$L^p$范数)是将向量映射到非负值的函数。向量x的范数衡量从原点到点x的距离，更严格地说，范数是满足下列性质的任意函数：
$$\bullet f\left(x\right)=0\Rightarrow x = 0$$
$$\bullet f\left(x+y\right) \le f\left(x\right)+f\left(y\right) \left({三角形不等式}\right)$$
$$\bullet \forall\alpha\in\Bbb{R},f\left(\alpha x\right)=|\alpha|f\left(x\right)$$
    当p=2时，$L^2$范数被称为欧几里得范数，表示从原点出发到向量x确定的点的欧几里得距离。$L^2$范数在机器学习中出现比较频繁，经常简化表示为$||x||\$。

    平方$L^2$范数对x中每个元素的导数只取决于对应的元素，而$L^2$范数对每个元素的导数却和整个向量相关。而它在原点附近增长得十分缓慢，区分恰好是零的元素和非零但值很小的元素是很重要的。我们转而使用在各个位置斜率相同，同时保持简单的数学形式的函数：$L^1$范数。可以化简为
$$||x||_{1} = \sum_i|x_{i}|$$
    as

RNN

RNN隐藏层神经元计算公式为 $ s_{t} = f\left( x_{t}U+s_{t-1}W \right) $ 其中U、W是网络的参数，f表示激活函数。RNN隐层神经元的计算由t时刻输入xt，t-1时刻隐层神经元激活st-1作为输入。

LSTM结构图

LSTM核心思想

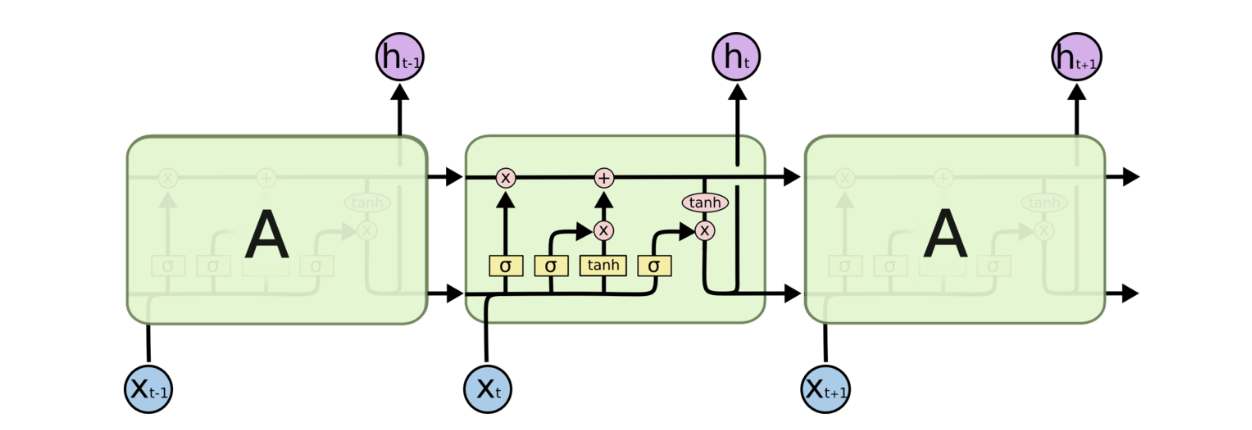
关键在于细胞状态，水平线在图上方贯穿运行，只有少量线性交互。LSTM拥有三个门，来保护和控制细胞状态。

对LSTM的理解

决定我们会从细胞状态中丢弃什么信息，该门会读取\(h_{t-1}\)和\(x_t\)，输出一个在0到1的数值给每个细胞状态\(c_{t-1}\)中的数字。回到语言模型的例子来基于已经看到的预测下一个词，可能包含当前主语的性别，因此正确的带刺可以被选择出来。

忘记门层

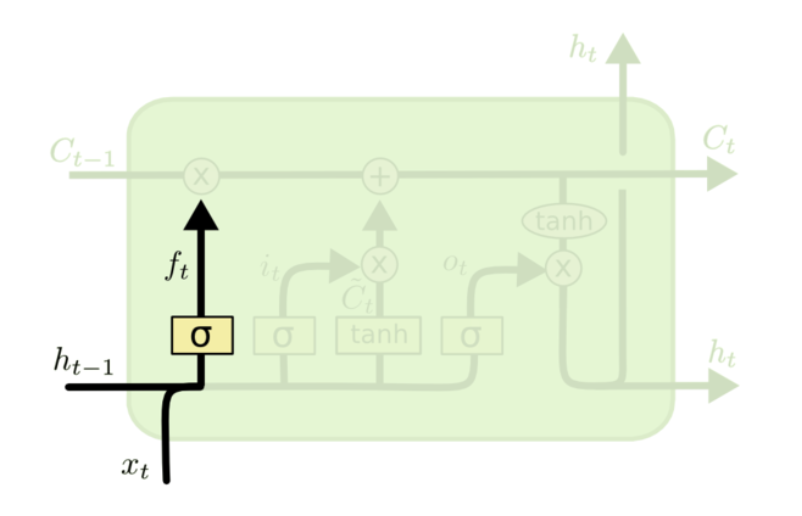
$f_{t}=\sigma\left(W_{f}\bullet[h_{t-1},x_{t}]+b_{f}\right)$

sigmoid层成“输入层”决定什么值我们将要更新，然后一个tanh层创建一个新的候选值向量，\(\tilde{C}_{t}\)会被加入到状态。

输入门层

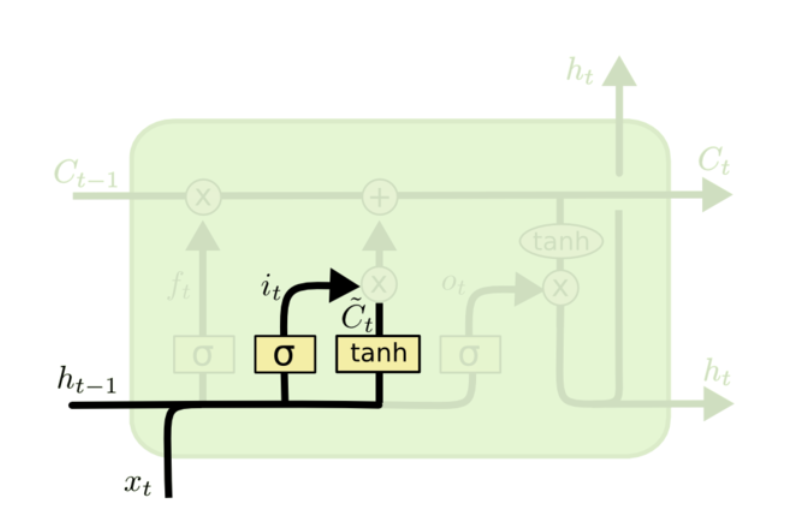
$i_{t}=\sigma\left(W_{i}\bullet[h_{t-1},x_{t}]+b_{i}\right)$

$\tilde{C}_{t}=tanh\left(W_{C}\bullet[h_{t-1},x_{t}]+b_{C}\right)$

更新细胞状态

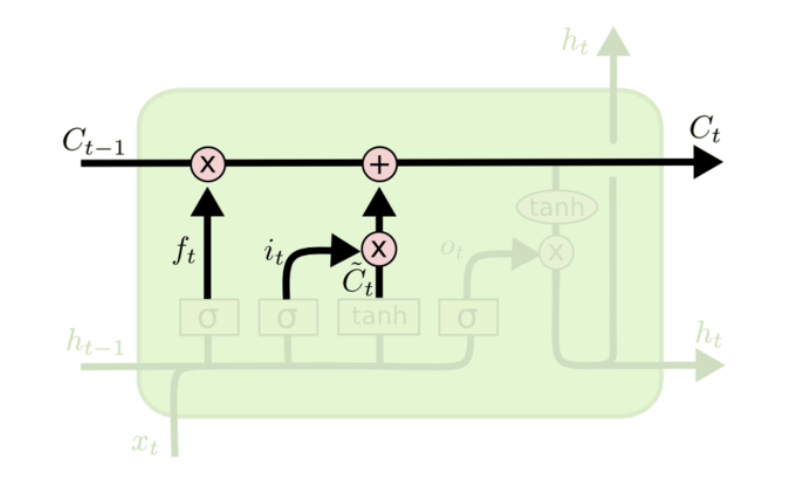
$C_{t}=f_{t}*C_{t-1}+i_{t}*\tilde{C}_{t}$
将$\tilde{C}_{t-1}$更新为$C_{t}$，把旧状态与$f_{t}$相乘，丢弃掉我们需要丢弃的信息，接着加上$i_{t}$和$\tilde{C}_{t}$这就是新的候选值。

输出层

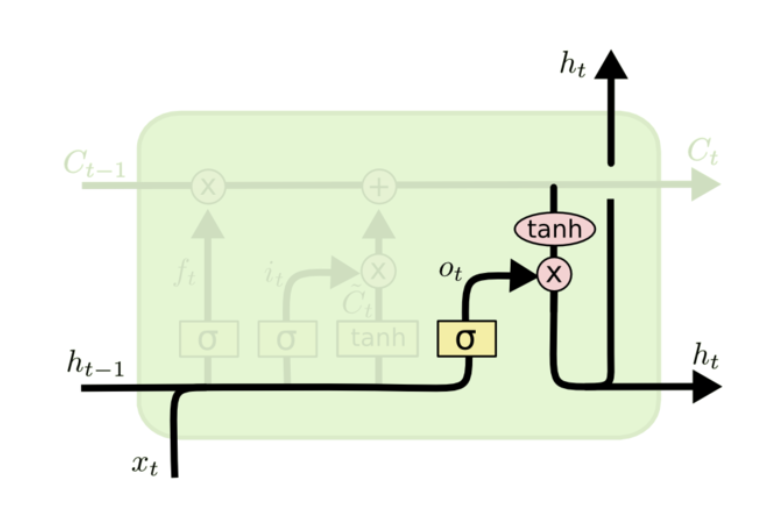
先运行一个sigmoid层来确定细胞状态的那个部分将输出出去，再通过tanh进行处理(得到一个在-1到1之间的值)并将它和sigmoid门的输出相乘，最终我们仅仅会输出我们确定输出的那部分。

LSTM前向传导

公式为

$i=\sigma\left( x_{t}U^i+S_{T-1}W^i \right)$

$f=\sigma\left(x_{t}U^f+s_{t-1}W^f\right)$

$o=\sigma\left(x_{t}U^o+s_{t-1}W^f\right)$

$g=tanh\left(x_{t}U^g+s_{t-1}W^g\right)$

$c_{t}=c_{t-1}\circ f+g\circ i$

$c_{t}=tanh\left(c_{t}\right) \circ o$

$tanh\left(x\right)=\frac{e^x-e-x}{e^x+e-x}$

to be continued…

多层感知机

激活函数的作用是将非线性引入神经元的输出。bais的作用是为每一个节点挺可训练的常量值。

前馈神经网络

• 输入节点：输入层，不进行任何计算，仅向隐藏节点传递信息
• 隐藏节点：隐含层，这些节点进行计算，并将信息从输入几点传递到输出节点，可以没有也可以有多个隐藏层
• 输出节点：输出层

在前馈网络中，信息只单向移动。

感知机

• 单层感知机：只能学习线性函数
• 多层感知机：可以学习非线性函数

反向传播算法

简单说，就是从错误中学习。最初，所有的边权重都是随机分配的，对于所有训练数据集的输入，人工神经网络都被激活，并且观察期输出。这些输出会和我们一致的、期望的输出进行比较，误差会传播到上一层。该误差会被标注，权重也会被相应的吊证。该流程重复，直到输出误差低于指定的标准。
在分类任务中，我们通常在感知器的输出才能好总使用softmax函数作为激活函数，以保证输出的是概率并且相加等于1.

• 向前传播：将训练样本作为输入，计算出输出层两个输出的概率值
• 反向传播和权重更新：计算出节点的总误差，并将这些误差用反向传播算法传播回网络中，以计算梯度。接下来使用类似梯度下降的算法来调整网络中的所有权重，目的是减少输出层的误差。

具体过程可以点击这里